1) Der Ahnherr Gustav Kirchhoff
Gustav Robert Kirchhoff (1824-1887), mit dessen berühmten Kirchhoffschen Regeln wir schon im Physikunterricht konfrontiert wurden, ist für uns insofern ein Ahnherr, als er eine Beschreibungstheorie einer klassischen Erklärungstheorie entgegenstellte. Kirchhoff wollte nicht mit Gesetzen Ursache-Wirkungszusammenhänge erklären. Er wollte beschreiben. Wir würden heute sagen, er wollte Modelle bilden. In dem schönen Aufsatz von R. Kötter und R. Inhetveen (1996) mit dem Titel „Beschreibungen in den Kultur-und Naturwissenschaften“ wird Kirchhoff wörtlich zitiert:
„Aus diesem Grund stelle ich es als die Aufgabe der Mechanik hin, die in der Natur vor sich gehenden Bewegungen zu beschreiben, und zwar vollständig und auf die einfachste Weise zu beschreiben. Ich will damit sagen, dass es sich nur darum handeln soll, anzugeben, welches die Erscheinungen sind, die stattfinden, nicht aber darum, ihre Ursachen zu ermitteln (G. Kirchhoff, Vorlesung über mathematische Physik, Bd. I, Leipzig 1876).“ Der Band I ist auch online verfügbar.
Kirchhoffs Jünger (WGIK 99) sprechen heute von Modellbildung und sehen diese als etwas ganz Wesentliches an. Modelle (Beschreibungen, Deskriptionen) sind für die Jünger wie Landkarten in einer unbekannten Landschaft, in der man sich ohne sie nur verirren kann. Die Bevölkerung kann kein Kartenlesen, und revoltiert manchmal gegen den eigenen Unverstand. Es beginnt dann auch das Lamento über den Bildungsmangel. Man verzweifelt in den Fernsehprogrammen, schon am einfachen Begriff „Reproduktionsfaktor“, obwohl das allgemeine Thema alle angeht.
Wir befassen uns exemplarisch mit dem bekannten SEIR-Modell und nehmen uns vor, demnächst auch den Agent-Based Models zu behandeln. Siehe in Sachen Corona die Arbeiten aus Hohenheim. Das SEIR-Modell ist aber grundlegend in der epidemiologischen Begriffsbildung. Wir verweisen an dieser Stelle schon auf unseren Erlanger Kollegen Reinhard German und seine Arbeit. Er hat mit seinen Kollegen zu beiden Modellgattungen intensiv geforscht. Auf Anfrage hat er mir erlaubt, seine bisher nur als Preprint (April 2020) erschienene Arbeit, die im Netz schon verfügbar ist, zitieren zu dürfen.
2) Das SEIR- Modell
Susceptible (anfällig) S,
Exposed (exponiert) E,
Infectious (infektiös) I,
Recovered (erholt) R.
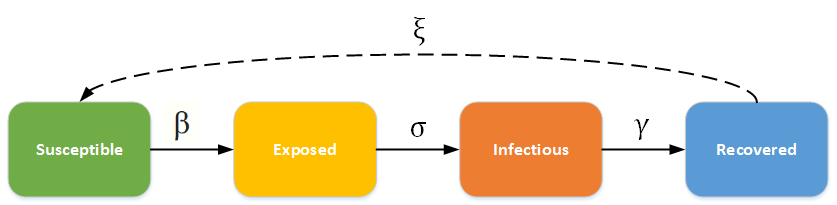
Bild 1: Zustände einer Epidemie und ihre Übergänge, aus: SEIR and SEIRS models
Das SEIR-Modell , sehr schön in Wikipedia beschrieben, lässt sich am besten als Zustands-Übergangsdiagramm (Bild1) darstellen. Zu Anfang eines epidemischen Durchlaufs bin ich im Zustand „anfällig“ oder S „Susceptible“. In S sind wir alle am Beginn einer Epidemie, alle in einer Population N (= 83 Millionen in Deutschland). Die Bevölkerungsgruppe S, die Anfälligen, geht mit einer gewissen Übergangsrate β in den Zustand E „Exposed“ (ausgesetzt, exponiert) über. Die in Gruppe E sollten möglichst schnell in die Quarantäne geschickt werden. Nach Ablauf einer Latenzzeit (Verzögerungszeit) kommt dann mit einer Rate σ heraus, ob ich mich angesteckt habe oder nicht. Habe ich mich angesteckt, bin ich im Zustand I „Infectious“. Mit einer Rate γ kann ich nach einem Test als geheilt gelten und wandere in den Zustand R „Recovered“ (erholt). Die Wiederansteckbarkeit mit der Rate ξ und die Rückführung auf den Zustand S ist im Falle der Corona-Epidemie noch in der Diskussion. Ich selbst habe als Kind zweimal Masern gehabt, 1943 und 1947. Die Masern sind also wiederansteckbar, in seltenen Fällen.
Rein in den Schlamassel gerate ich mit der Rate β, heraus komme ich mit der Rate γ.
Das Verhältnis: R0 = β / γ (oder „Rein“ dividiert durch „Raus“)
ist die bekannte Basisreproduktionszahl, von der im Fernsehen als Variable dauernd berichtet wird. In S E I R von Wikipedia wird R0 sehr schön abgeleitet (Seite 3). R0 < 1 bedeutet, dass mehr „Raus“ gehen als „Rein“, ein anzustrebender Zustand. Wehe es geschieht, dass in einer zweiten Welle R0 > 1 wird. Dann hat man mehr „Rein“ als „Raus“ und die Epidemie ist nicht mehr im Griff. Das müsste doch eigentlich jeder verstehen, auch mit mäßiger Schulbildung. Demonstrationen sind entbehrlich.
S E I R sind relative Zahlen, relativ in Bezug auf die Gesamtpopulation N, deren Individuen sich in einem der vier Zustände befinden. Das heißt:
S + E + I + R = 1 (relativ) und
NS + NE + NI + NR = N (absolut)
Das sind vier Bevölkerungsgruppen, die epidemiologisch zur Debatte stehen. S=1 ist ein Idealzustand (epidemiefrei), weil dann E, I, R = 0 sind.
Wichtig ist nun, die zeitlichen Verläufe von S, E, I und R zu kennen. Man bezeichnet die Verläufe mit S (t), E(t), I(t) und R(t) und meint damit das dynamische Geschehen der Epidemie in der Bevölkerung. Man benötigt z.B. den Differentialquotienten dS / dt, also Änderungstendenz dS und Änderungsstrecke dt, was dem Steigmaß (Veränderungsmaß) an der Kurve S(t) entspricht.
Wo man in der Literatur über SEIR hinschaut, es werden einem vier Differentialgleichungen (DGL) als System präsentiert, die wir unten wiedergeben, ohne Kommentar. Denn wir wollen beim Leser keine Kenntnisse in der höheren Mathematik voraussetzen. Der Leser sei auf die Literatur z.B. SEIR and SEIRS models verwiesen. Für uns ist es hier nur wichtig herauszustellen, dass Differentialgleichungen (DGL) ein bedeutungsvolles Hilfsmittel in der dynamischen Beschreibung naturwissenschaftlicher, ökonomischer und biologischer Zusammenhänge sind. Ob man Mathematik mag oder nicht, ist unerheblich.
In SEIR wird sogar beispielhaft eine Lösung dieses Gleichungssystem vorgeschlagen, wobei die Daten von COVID -19 2020 für Deutschland zur Grundlage gemacht wurden. Man nimmt bei der Ausbreitung der Epidemie die Basisreproduktionszahl R0 = 2,4 an, was einer Unterlassung wesentlicher Quarantäne-Maßnahmen entspricht.
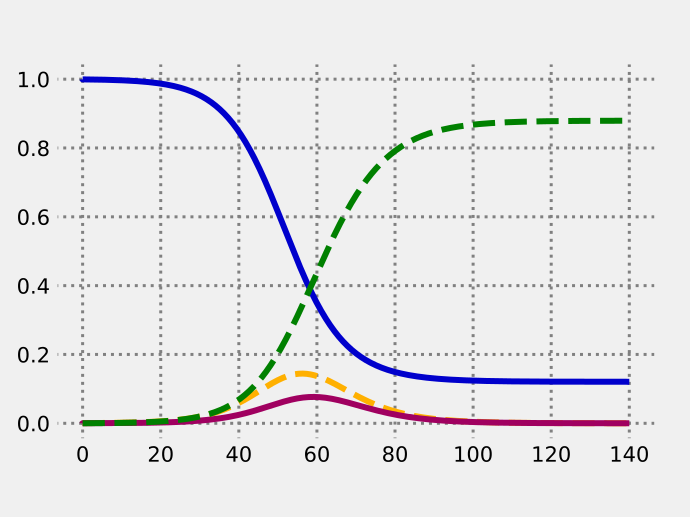
Die vier Anteile, jeweils abhängig von der Zeit in Tagen.
S in Blau, E in Gelb gestrichelt, I in Magenta, R in Grün gestrichelt.
Bild 2: Zeitlicher Verlauf der Komponenten, aus SEIR Seite 9
Die Kurve für I (Magenta), die Kurve der Infizierten, erreicht nach 60 Tagen eine Kulmination von rund 0,1 oder 10 % der Bevölkerung von 83 Millionen, das sind rund 8 Millionen Patienten. Die Kapazität in deutschen Kliniken für Qurantäne-Patienten wäre vollkommen überfordert.
Wir haben uns nur mit dem SEIR als Standard-Modell befasst. Eine wesentliche Erweiterung von SEIR ist in der Arbeit vom Kollegen German zu finden (siehe insbesondere Figure 1). Unser Anliegen war ein exemplarisches Beschreiben im Sinne von Gustav Kirchhoff.

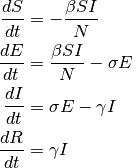
Interessante und plausible Erläuterung zum Epedemiegeschehen.
Ich vermisse als Laie aber im SEIR-Modell einen Abzweig für die Toten (als Differenz zwischen I und R ?) , damit das ganze Gleichungssystem wie in einem Strömungsmodell auch aufgeht.
Eine Erweiterung des SEIR-Modells mit Toten findet man in der zitierten Arbeit von German. Siehe in dieser Arbeit z.B. „Figure1“. Für eine Behandlung eines erweiterten SEIR-Modells ist ein Blog ungeeignet, weil viel zu kompliziert. Das ist die Angelegenheit eines wissenschaftlichen Artikels. Ein Blog ist ja nur so etwas wie eine Zeitung und fordert zur Bescheidenheit auf, weil der Leserkreis keine spezifische Vorbildung haben kann.
Ihr
Hartmut Wedekind
Saved as a favorite, I really like your blog!
Hey there! This is my 1st comment here so I just wanted to give a
quick shout out and say I really enjoy reading through your articles.
Can you recommend any other blogs/websites/forums that go over the same topics?
Thanks a lot!
I recommend the blog of my colleague Albert Endres: http://bertalsblog.blogspot.com/
The blog is much more extensive than mine.
Hartmut Wedekind
It’s really very complex in this active life to listen news on TV, therefore I just use the web for that reason, and take the
hottest information.
Thanks in favor of sharing such a fastidious opinion,
post is nice, thats why i have read it completely