1) Entwicklung eines Schemas „Sortieren durch Einfügen“.

Tänzer nach Schema (Choreographie) „Sortieren durch Einfügen“

Wir kommen zurück auf unsere Sortieraufgabe, dargestellt durch Tänzer.

a(0) = 3, a(1) = 0, a(2) = 1, a(3) = 8, a(4) = 7, a(5) = 2, a(6) = 5, a(7) = 4, a (8) = 9, a(9) = 6

Wenn ich tanzende Menschen in einer gewissen Ordnung sehe, stelle ich mir mit meinen Schülern zunächst einmal die Frage, wie bringe ich die Wechsel-Bewegungen der Tanzenden als Schema in eine symbolische Form. Offensichtlich wird ja ganz zu Anfang aus a(0) = 3, a(1) = 0 eine Vertauschung durch Bewegung mit dem Ergebnis: a(0) = 0, a(1) = 3. Die Bewegung findet statt, weil ‚0’ kleiner als ‚3‘ ist und somit die ‚0‘ in einer sortierten Folge vor die ‚3` zu stehen kommt. Die ‚0‘ wandert auf die 1.Position von links und die ‚3‘ auf die 2. Position. Einfacher geschrieben: wie mache ich aus einer Folge 3,0 eine Folge 0,3.

Wir schrieben das „von Hand“ hin. Der Witz einer Digitalisierung ist aber, dass ein Digitalrechner u.a. menschliche Handlungen übernimmt. Und der Mensch kann zuschauen. Was wir brauchen ist ein Handlungsschema, das der Digitalrechner versteht, d.h. umsetzen kann. Wie sieht so ein Handlungsschema aus? Es besteht im Kern aus Anweisungen (instructions), denen der Rechner folgen muss. Leider kann man sagen, wird eine solche Anweisung in den meisten Sprachen durch ein Gleichheitszeichen (=) wiedergegeben, was eine „Sünde wider den Heiligen Geist“ ist, weil dieses Zeichen schon eine Gleichheit (Äquivalenz) darstellt. x= 5 als Anweisung bedeutet nicht “die Variable x ist gleich 5“. Das wäre eine Aussage. In einer logischen Propädeutik haben wir aber gelernt, dass eine Aussage (proposition), die z.B. wahr, falsch oder unbestimmt sein kann, grundsätzlich von einer Aufforderung (request) zum Handeln unterschieden werden muss. In einem Handlungsschema ist x= 5 als eine Aufforderung oder als eine Anweisung an den Rechner zu verstehen: “Bitte, lieber Rechner, mache das die ganze Zahl ‚5‘ der Variablen x zugewiesen wird. Statt „Bitte“, wie im höflichen Leben, könnte man auch sagen wie auf dem Kasernenhof: „Ich befehle dir, für x den Wert ‚5‘ anzunehmen“. Man schreibt dann auch in logischen Zusammenhängen „! x=5“, mit ‚!‘ als dem Aufforderungssymbol oder Appellator.  Aber das Zeichen ‚!‘  kennt man in der Welt der Programmierung leider nicht, weil man sich, wie gesagt, einer „Sünde wider den Heiligen Geist“ schuldig gemacht hat.  Eine hübsche Nebenbemerkung: „Kasernenhof-Programmiersprachen“ nennt man auch imperative Programmiersprachen. „Imperativ“, das ist in der Grammatik die Befehlsform. Der Indikativ, der andere grammatische Modus, steht für Aussagen zur Verfügung. Und der dritte Modus, der Konjunktiv, der Modus des Möglichen, den gibt es in der Programmierung aus ersichtlichen Gründen nicht.

Wie geht das nun, das Vertauschen schematisch vor sich: ‚0‘ an zweiter Stelle nennen wir den Austauschkandidaten, für den Platz geschaffen werden muss. Der Austauschkandidat a(1) =0 muss gesichert werden, weil gleich der Nachrücker a(0) = 3 diesen Platz einnehmen will.  Wir definieren eine Variable vom Typ ‚integer‘, nennen sie ‚kandidat‘ und schreiben die Anweisung hin:

(1)      kandidat = a(1);

Jetzt ist die ‚0‘ beiseite geschafft, gespeichert und kann nicht mehr verlorengehen. Nunmehr darf ich die Anweisung erteilen:

(2)      a(1) = a(0);

und schon steht ‚3‘ aus a(0) = 3 auf dem Platz a(1) , wo vorher die ‚0“ stand. Wir dürfen jetzt aber nicht vergessen, die ‚0‘ auf den Platz a(0) zu bringen. Wir tun das, indem wir schreiben:

(3)      a(0) = kanditat;

Hurra, wir haben das Problem im Prinzip im Partikularen mit den drei Anweisungen (1); (2); (3) gelöst. Ein Semikolon (;) soll ein Hintereinander abgeschlossener Anweisungen bedeuten. Wir müssen die Lösung aber noch für die ganze Folge verallgemeinern. Denn wir wissen, das Generische, das Allgemeine ist der Kern einer Schemabildung in der Programmierung.

Bild 1: Schema von „Sortieren durch Einfügen“ als Struktogramm.

In einem Struktogramm dürfen keine Symbole verwendet werde, die später in Programmiersprachen auftauchen. Das Semikolon (;) z.B. hinter einer Anweisung ist verboten. Das riecht nach der Programmiersprache Java.

Das Schema in Bild 1 zeigt zwei Vorgänge.  Einmal den Zähl-Vorgang, der die Bewegung von i = 1 bis n  darstellt. Das ist die Vorwärtsbewegung der Tänzer von links nach rechts.  Und dann der Einfüge-Vorgang, wenn ein Element größer als der Kandidat ist. Zentral für die Programmierung ist, dass man das nicht, wie in unserem speziellen Fall, n = 10 mal hinschreibt, was stink-langweilig wäre, sondern eine Zähl-Schleife und eine Solange -Schleife vorsieht. Schleifen (loops) sind in der Programmierung ganz wichtig. Der Digitalrechner liebt den Stumpfsinn, im „Kreis“ herumzulaufen. Für den Stumpfsinn ist er ja geschaffen worden. In den Schleifenköpfen werden die Bedingungen angegeben, die für die Ausführung der Schleifen gelten. Eine Schleife wird verlassen, wenn die Bedingungen im Kopf der Schleife nicht mehr zutreffen. Man spricht von einer Endlos-Schleife, wenn man aus der Schleife überhaupt nicht mehr herauskommt. Das ist dann ein Fehler. In der Echtzeit-Programmierung (Kontroll-Programmierung) setzt man aber manchmal absichtlich Endlos-Schleifen ein, wenn z. B. bei Kontrollgängen in der Fertigung immer wieder am Anfang begonnen werden muss. „Until doomsday“, bis zum jüngsten Tag sagt man in der manchmal „eschatologischen“ Sprache der  Programmierung. Der jüngste Tag ereignet sich aber z.B., wenn der Rechner abgeschaltet wird. Ohne Strom  geht nichts mehr. Ohne Strom global ist auch die ganze  Digitalisierung am Ende.

2) Konkretion eines Schemas

Aus der Logischen Propädeutik ist bekannt, dass Konkretion und Abstraktion umkehrbare (reversible) Operationen sind. Das ist wie bei der Kehrwertbildung. Der Kehrwert von a ist 1/a, und der Kehrwert von 1/a ist wieder a. Im Allgemeinen ist es so, dass eine Abstraktion einer Konkretion methodisch vorausgeht. Erst kommt das Konkrete und dann das Abstrakte, z.B. erst kommen die Ziffern und dann die Zahlen.

In der Pädagogik haben wir eine Sondersituation, eine Lehr-Lernsituation, und da ist die Sachlage anders. Der Lehrer muss vormachen, „zeigen“ würde der berühmteste aller Volkschullehrer Ludwig Wittgenstein (1889 – 1951) sagen, und der Schüler muss nachmachen, was der Lehrer zeigt. In der Pädagogik gilt der Grundsatz: Erst kommt das Leichte und dann das Schwierige. Wer gegen diesen Grundsatz verstößt, begeht einen Kardinalfehler; das ist ein Fehler, der eine „gestellte Aufgabe komplett unlösbar macht“.

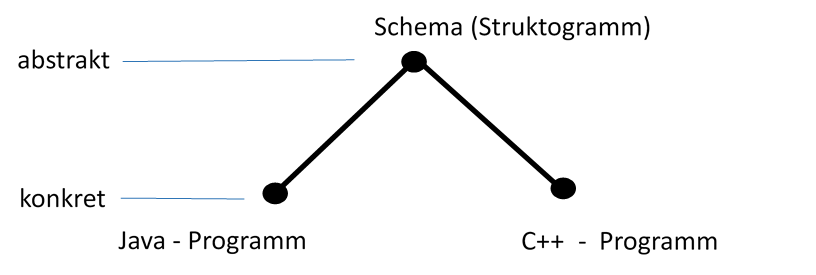
Nun ist es so: Ein Schemaentwicklung, die wir am Beispiel „Sortieren durch Einfügen“ betrieben haben,   ist wesentlich  leichter  als eine Programmentwicklung, allein schon, weil   der große syntaktische Ballast einer Programmiersprache  mitgeschleppt werden muss. Wir nehmen aber mal an, es lägen uns schon für unser „Sortieren durch Einfügen“ zwei fertige Programme in den berühmten Programmiersprachen „Java“ und „C++“ vor. Die beiden Programme folgen natürlich auch einem Schema, und das ist genau unser entwickeltes Schema. Das Schema ist das Abstrakte, „Java“ und „C++“ hingegen sind das Konkrete. Wir dürfen die folgende Gleichung hinschreiben:

Für „Sortieren durch Einfügen“ gilt:

„Das Schema des Java-Programms = Das Schema des C++-Programms.“

Das Gleichheitszeichen ‚=‘ wird „schemagleich“ genannt und ist eine Äquivalenzrelation, also ist sie reflexiv, symmetrisch und transitiv, wie wir aus der logischen Propädeutik wissen. „Schema“ ist das Abstrakte“. Die Darstellungen in Programmiersprachen sind das Konkrete.

Im Beitrag „Marx heute“  war die Abstraktion entsprechend. Hier schrieben wir frei nach Karl Marx:

„Der Wert eines Quarters Weizen = Der Wert von a Ztr. Eisen“, mit ‚a‘ als einem schematischem Buchstaben.

Abstrakt bei Marx  ist der Wert (Tauschwert), konkret sind Weizen und Eisen. „Weizen“ übernimmt in der Entsprechung  die Rolle von Java, „Eisen“ die Rolle von C++ und „Wert“ die Rolle von Schema. Das hört sich bizarr an. Ist es auch. Abstraktion ist eben nur eine „facon de parler“  (eine neue Art zu sprechen oder Symbole auszutauschen, aber eine  verdammt wichtige Art).

Bild 2: Abstraktion und Konkretion

Eine Konkretion unseres Schemas „Sortieren durch Einfügen“ in einem Java – Programm entnehmen wir aus Java Programmieren :

Bild 3 : Java – Programm „Sortieren durch Einfügen“

Es ist eigentlich sehr leicht, den logischen Kern in Bild 3,  also das Schema eines solchen Textes bloßzulegen. Die Schlüsselbegriffe (key terms) der Sprache „Java“  sind englisch. Die Begriffe der Anwendung in Bild 3  sind  deutsch. Das Bloßlegen des Kerns kann man heute schon mittels Software à la Easy Code  erledigen lassen, um im Schema  Veränderungen (Editieren) vorzunehmen.

3) Schlussbetrachtung

Im Zeitalter der Digitalisierung gehört das Thema eines Programmier-Unterrichts bis hin zu einer Schemaentwicklung sicherlich zu einem wichtigen  Bildungsgut. Ob man auch noch tiefer in die Programmierung  auf der Sekundarstufe 1  durch  Erlernen  des Grundgerüstes einer modernen Programmiersprache einsteigt, z.B. Java, C++ oder auch die viel gelobte Sprache Python, hängt von den örtlichen Gegebenheiten, insbesondere aber von den Schülern ab. Denn wie sagt uns unser  große Dichter Johann Wolfang von Goethe (1749-1832) so aufmunternd: „Lust und Liebe sind die Fittiche zu großen Taten“.  „Der Tragödie 2.Teil“ ist auch ein Ausdruck, der vom großen Goethe (Faust 2) stammt. Es handelt sich bei uns um eine Tragödie,  weil es einen Programmier-Unterricht voraussetzungslos nicht geben kann. Meine mir im Traum   zugeteilte Lehraufgabe gebe ich gerne zurück. Tragödien sind nicht mein Fach. Lehraufgaben  mit dem Thema „Logische  Propädeutik der Informatik“ nehme ich auch heute noch  gerne entgegen. Ohne Logische Propädeutik kein Programmier-Unterricht !