Antragssteller

Dr. Fabian Wein
Zentralinstitut Scientific Computing
FAU Erlangen-Nürnberg

Projektübersicht

The academic finite element simulation software CFS++ (Coupled Field Simulation with CFS++) had been enhanced by MPI parallel linear system solvers based on the PETSc library. This gives immediate access to a broad range of linear system solvers provided by the framework, where state-of-the-art algebraic multilevel solvers are most beneficial.

The major workload for typical finite element simulation in CFS++ is the solution of linear systems. Implementing the PETSc framework offers a wide range of specialized MPI-parallel solvers for linear systems. In contrast to already integrated OpenMP based packages like LIS (Library of Iterative Solvers for Linear Systems), SuiteSparse/CHOLMOD or PARDISO, the integration of an MPI-based package required significant modification of the framework.

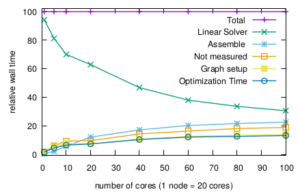
Fig. 1 shows, that the impact of the linear solver in total run time can be significantly reduced. In the present example, only systems of equations with 3×10^6 unknowns are solved, the high number of cores/ nodes on the Emmy compute cluster would benefit from larger systems. Clearly, also Amdahl’s law applies in that not yet serialized parts of the software become significant. To mention two, graph setup of the sparse matrix system and assembling the finite element stiffness matrix, both can significantly benefit from MPI-parallelization, as the potential of OpenMP parallelization in these two tasks is memory bounded and requires time-consuming memory access control. Both, graph setup and assembling are already experimentally reimplemented based on the PETSc framework, but the full parallelization is still subject to future work as it requires the partition and distribution of the finite element mesh and the calculation of local finite element matrices.