Antragssteller
Prof. Dr. Ernst Rank
Computation in Engineering
TU München
Projektbericht
Numerical methods play a central role in the design and development of processes and products in engineering practice. One such technique is the finite cell method (FCM), a variant of the finite element method (FEM) that is suitable for performing numerical simulations on bodies with complex geometries. FCM simplifies the process of mesh generation for complex geometries while at the same time providing high accuracy by combining a fictitious domain approach with high-order finite elements.
This project aimed at improving the parallel performance of AdhoC++, an advanced high-order FEM/FCM code in order to allow efficient computations of problems of engineering relevance on modern HPC systems. AdhoC++ is written in C++ and is developed and maintained by the Chair for Computation in Engineering at the Technical University of Munich. It contains a series of numerical modules that facilitate FE computations in the field of solid and structural mechanics. It’s core features include, (1) The use of high-order finite elements, (2) the finite cell method that allows a unified treatment of different geometrical models and (3) the use a flexible hp-refinement scheme that allows
easy mesh adaptation in two and three dimensions.
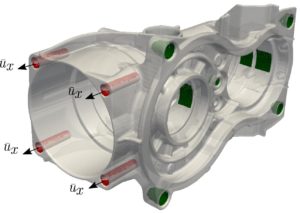
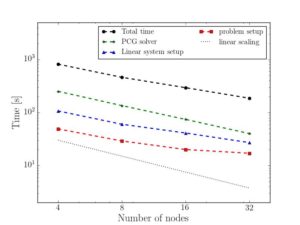Figure 1: Geometry and scaling results of a linear elasto-static simulation. The computa- tional mesh T h comprises 89,000 hexahedral elements with a polynomial order p = 4 and a total of 3.9 million unknowns. Hybrid simulations are run on the Linux-cluster at the LRZ. In each simulation 4 MPI tasks @ 7 OpenMP threads are run per node. This linear elastic investigates the effect of pores in parts produced by die casting.
AdhoC++ was originally designed as a shared-memory (OpenMP) code. The necessity of exploiting the codes capabilities in large engineering applications initiated the first attempt for an MPI parallel version of the code in 2015. The chosen parallelization strategy entailed a globally replicated mesh data structure that was present on every MPI task. This approach was at the time advantageous due to its simplicity, low communication costs and straight-forward mesh refinement strategies. Its major bottleneck, however, was its high memory consumption due to the replication of the total mesh data structure on every process. As a result, parallel computations were only possible on clusters with
a large amount of memory per core.
The two major objectives of this KONWIHR project were to ov ercome the memory limitations of the code and port it to modern HPC systems such as the Linux Cluster at the Leibniz Center for Supercomputing (LRZ). This was to be achieved in three project phases. Phase one would tackle the code’s node-level performance with special focus on AdhoC++’s memory footprint. The second phase would involved the implementation of a distributed mesh data structure while the third project phase would be centered on the improvement of the linear system solver and the implementation of a matrix-free solution approach for the finite cell method.
This project succeeded in porting the finite element code AdhoC++ to the Linux cluster at the LRZ. Major code-bottlenecks were addressed and a distributed mesh data structure tailored to the needs of the code was implemented and tested in a complex 3-dimensional engineering example from the field of solid mechanics. A fully parallel simulation pipeline in AdhoC++ from the pre-processing phase up to the post-processing is the result of all the code modifications. With this modifications it is now the possible to compute examples of engineering relevance such as the example shown in Figure 1.
The Chair of Computation in Engineering is grateful for the collaboration with the CFDLab team at LRZ and for the financial support from KONWIHR without which this work would not have been possible.