1) Gegenläufige Tendenzen in Sachen Gesundheit und Wirtschaft/Bildung

In den Jahren 2020/21 kämpfen wir überall auf der Welt mit der Corona – Pandemie. Es gibt nur zwei Mittel in diesem Kampf. Die klassische Isolation (I1) der Menschen, um Ansteckungen zu vermeiden, und die moderne Impfung (I2). Tagesfrage seit Langem ist, ob es einen optimalen Einsatz dieser „Waffen“ gibt. Unsere Antwort wird sein: Ja, es gibt einen solchen optimalen Einsatz. Leider nur erstmal auf dem Papier, also reine Theorie, mehr nicht. Aber das ist auch schon etwas, und könnte unsere Gedanken leiten. Für uns in unserem Blog „Unsere Zeit in Gedanken fassen“, ist etwas auch auf Papier schon  etwas wert. Gedanken entstehen eben auf dem Papier. Und darüber hinaus ist es auch ganz einfach, was wir zu sagen haben. Denn es liegt ein allbekanntes, klassisches Optimierungsproblem vor uns, wenn wir unsere missliche Lage mit Abstand betrachten.

Für „Isolation“ benutzt man im Deutschen auch den englischen Ausdruck „stutdown“ (schließen), und wenn man in Gedanken den Schlüssel auch noch herumdreht, sagt man verschärft „lockdown“ (zusperren). Das klingt nach Haft in einer Zelle.

Wer es mit gegenläufigen Tendenzen (opposed tendencies) zu tun hat, sucht einen optimalen Ausgleich. Im Amerikanischen sagt man „trade-off“ und meint so etwas wie einen Kompromiss, einen Deal, den zwei Kontrahenten miteinander eingehen. Wer sein Haus beispielsweise isolieren will, um Geld zu sparen, weiß um eine Gegenläufigkeit. Er kann beliebig viel Geld in die Wärme-Dämmung stecken, um seinen Energieverbrauch zu reduzieren. Die Kosten für die Dämmung gehen hoch, während sich die Energiekosten vermindern. Wo ist die kostenoptimale Dämmung, der optimale Tradeoff in diesem „Deal“?

Schwieriger als beim Häuser-Dämmen, ist die Frage nach einem Tradeoff in unserem Pandemie-Problem. Es sind Erfahrungstatsachen, dass mit zunehmender Isolation der Menschen die Kontakte und damit die epidemischen Ansteckungen und ihre Kosten vermindert werden, während die Kosten in Wirtschaft und Bildung ansteigen. Unser Tagesproblem lautet: Wo ist der Tradeoff, der Kompromiss, möglichst optimal, also bestmöglich.

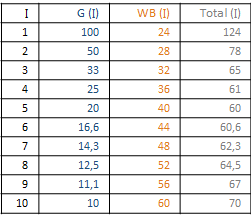
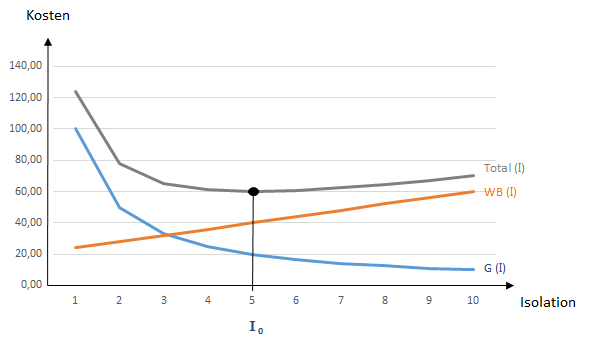
Bild 1:  Optimale Isolation in einer Pandemie

Wir konzentrieren uns auf Bild 1 nebst Wertetabelle.

Die Kosten der Wirtschaft und Bildung WB(I) werden ganz gemächlich linear über dem Grad der Isolation I aufgetragen. Der Verlauf ist eine Annahme. Für die gegenläufige Größe „Gesundheit“ G(I) wird über der Isolation I ein rapider Abfall angenommen. Es ist ein parabolischer Abfall. Noch drastischer wäre ein exponentielles Schrumpfen, das bei den pandemischen Infektionen sehr realistisch ist. Darüber wird die wichtige Summe WB(I) + G(I) = Total (I) aufgetragen. Die Kurve hat für I₀ = 5 ihr Optimum. Der Verlauf ist sehr flach. Das liegt daran, dass wir einen sehr sanften linearen Kostenanstieg für Wirtschaft und Bildung angenommen haben. Das Resultat für TOTAL(I) ist deshalb eine flache Rinne und kein U-förmiger Trinkbecher. Den können wir aber leicht erzeugen, indem wir einen starken Kostenanstieg für Wirtschaft und Bildung WB(I) ins Kalkül ziehen. Nach I₀ = 5 kippen wir so den rechten Ast in Bild 1 nach oben, so dass eine Becherform entsteht. I₀ wird durch die Steig- bzw. Schrumpfungsmaße bestimmt. Das weiß man, seit es Differentialrechnung gibt.

Was wir sagen wollen ist folgendes: Eine flache Kurve für Total (I), wie in unserem Beispiel, ist erstrebenswert, weil dann ein Schätzfehler bei statistischen Größen nicht so übelgenommen wird. Der Verlauf ist robust, aber heute unrealistisch. Ein steiler Anstieg von Total(I) nach links und rechts vom Optimum I₀ wäre verheerend und entspricht wohl mehr unserer heutigen Situation. Der zentrale Punkt für Politiker sind Kenntnisse der Steig- und Schrumpfungsmaße, die das Optimum I₀ und seine Umgebung bestimmen.  Ob unsere Politiker das wissen? Wüsste ich es, wenn ich Politiker wäre? Was wir brauchen sind „trade-off politicians“, also Politiker, die in Tradeoffs, also in Gegenläufigkeiten denken können. Ideologen können das nicht.

Wenn wir annehmen, dass eine Impfung der Bevölkerung einen konstanten Abzug K von den Gesundheitskosten bedeutet, also WB(I) + G(I) – K = Total(I), dann ist eine Impfung für ein Optimum I₀ unerheblich, weil keine Konstanten, sondern nur Schrumpf- und Steigmaße bei der Bestimmung eines Optimums eingehen. Testen ist ein Effektiver-Machen eines Isolationsverfahrens. Man weiß halt mehr über die Verbreitung des Virus.

2) Virologie und Epidemiologie gegen Ökonomie und Bildung

Der Kampf ist angesagt. Gewinnen können beide Seiten nur, wenn das Virus verschwindet. Bis das der Fall ist, muss versucht werden, zu „überwintern“. Und dazu gehört das Bewusstsein, dass es so etwas wie eine günstigste Isolation existiert. Man muss übervolle Krankenhäuser mit ihren Intensivstationen und nachhaltigen Gesundheitsschäden sogar mit Todesfällen auf der einen Seite mit leeren Geschäften, abgesagten Veranstaltungen und leeren Bildungsanstalten vergleichen können. Und das tut ja jemand, der wie wir an einen besonders günstigen Weg aus der Kalamität denkt. Die optimale Isolierung eines Hauses ist eine vergleichsweise simple Aufgabe. Und doch sind beide Probleme ähnlich. Es sind eben Tradeoff- oder Kompromiss-Probleme, die auf der Isolationsachse sichtbar werden. Was gewinnt man an Ökonomie und Bildung, wenn die Isolation um eine Einheit zurückgeführt wird, und was verliert man im Hinblick auf den Gesundheitszustand der Bevölkerung dabei?

Man erkennt sofort, dass das eine interdisziplinäre Fragestellung ist, die z.B. ein Epidemiologe alleine nicht beantworten kann. Der Politik bleibt nichts anderes übrig, als auf Sicht zu fahren und zu probieren (trial and error). Alles ist erlaubt, nur keine einseitige Ideologie, die eine der beiden Seiten favorisiert. Man landet dann an den Rändern der U-förmigen Kurve, ohne Tradeoff und Ausgleich. Wichtig ist, dass man sich auf dem Talboden aufhält und immer an die Möglichkeit eines Optimums denkt.