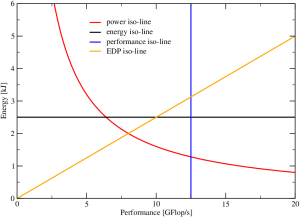
Energy consumption and power dissipation have become the latest craze in HPC, for several reasons. Unfortunately there is also a lot of confusion about the interplay of performance and power. Thomas Zeiser from the RRZE HPC group has come up with an interesting way of visualizing energy-performance data on the CPU socket level that makes it easier to reason about energy consumption. The Z-plot shows dissipated energy to solution (i.e., how much energy is spent for solving a given problem) versus the program’s performance, which can be quantified by any appropriate metric that is inversely proportional to the runtime. Figure 1 shows that, if we always solve the same problem, most of the interesting quantities one would like to study in the Z-plot are constant along some simple line: obviously, all program runs with the same energy lie on a horizontal line (black), and all runs with the same performance lie on a vertical (blue), but also all runs with the same energy-delay product (EDP) lie on a straight line through the origin (orange), the slope of the line being proportional to the EDP. Finally, all runs with the same power dissipation lie on a hyperbola (red). If we change something, such as the number of active cores per chip or the clock speed, or if we optimize or otherwise change the code, it is insightful to see how different metrics change as we move through the Z-plot. As a first example we study the behavior of a scalable code on a multi-core CPU socket.
Scalable performance vs. active cores
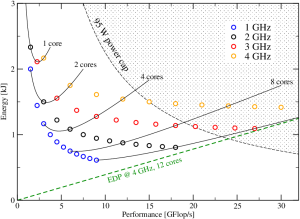
Figure 2: A scalable program in the Z-plot. Each circle represents a run at a certain clock speed (color coded) and a given number of cores. The solid lines interpolate between points with the same number of cores, i.e., the clock speed changes continuously along the line.
A good definition of “scalable” in a multicore context is “performance is linear in the number of active cores n.” Usually such programs also scale linearly in the clock speed f; the performance can thus be described by P(n,f)=nP_0f/f_0~~,where f_0 is some base or reference clock speed. If we run such a code on a multicore CPU, varying the number of cores and the clock speed, we may get data as shown in Figure 2. Some important observations strike the eye:
- The more cores we use at a given clock speed (same-color data points from left to right), the lower the energy to solution.
- Increasing the clock speed at constant number of cores seems to always increase the energy for large core counts, but for smaller core count there appears to be an optimal clock speed at which energy is at a minimum. This optimal frequency goes up as the number of cores goes down. E.g., it is around 3 GHz at one core but below 2 GHz at four cores.
- The energy-delay product (EDP) goes down as the frequency goes up at fixed core count. In our example it is lowest at 12 cores and 4 GHz (green dashed line).
The data in Figure 2 does not come from measurements; it was constructed from the combination of our “scalable performance” model above with a multi-core power model, which was introduced in [1]. In a follow-up post I will show some measurements on real systems. In [2] we have applied the model to a lattice-Boltzmann (LBM) solver, but LBM is non-scalable across cores, which requires special treatment. Stay tuned.
[1] G. Hager, J. Treibig, J. Habich, and G. Wellein: Exploring performance and power properties of modern multicore chips via simple machine models. Concurrency and Computation: Practice and Experience, DOI: 10.1002/cpe.3180 (2014). Preprint: arXiv:1208.2908
[2] M. Wittmann, G. Hager, T. Zeiser, J. Treibig, and G. Wellein: Chip-level and multi-node analysis of energy-optimized lattice-Boltzmann CFD simulations. Concurrency and Computation: Practice and Experience, DOI: 10.1002/cpe.3489 (2015). Preprint: arXiv:1304.7664