We use the Schönauer Vector Triad for most of our microbenchmarking. It’s a simple benchmark that everyone can write. It looks quite simple when parallelized with OpenMP:

double precision, dimension(N) :: a,b,c,d
! initialization etc. omitted
s = walltime()
!$omp parallel private(R,i)
do R=1,NITER
!$omp do
  do i=1,N
    a(i) = b(i) + c(i) * d(i)
  enddo
!$omp end do
enddo
!$omp end parallel
e=walltime()
MFlops = R*N/(e-s)/1.e6

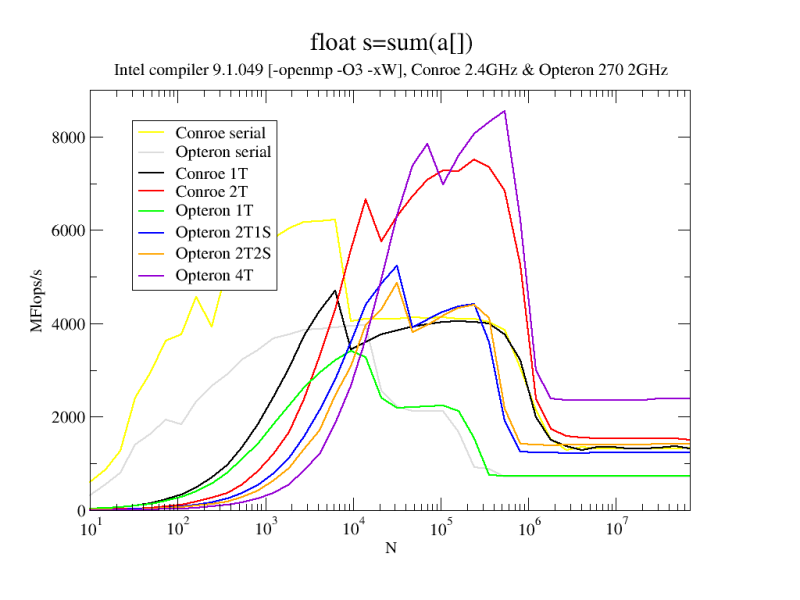
There are some details that are necessary to make it work as intended; you can read all about this in our book [1]. Usually we choose NITER for every N so that the runtime is a couple hundred milliseconds (so it can be measured accurately), and report performance for N ranging from small to large. The performance of the vector triad is determined by the data transfers, even when the data is in the L1 cache. In the parallel case we can additionally see the usual multicore bandwidth bottleneck(s).

The OpenMP parallelization adds its own overhead, of course. As it turns out, it is mostly concentrated in the implicit barrier at the end of the workshared loop in this case. So, when looking at the performance of the OpenMP code vs. N, we usually see that using more threads slows down the code if N is too small. We can even calculate the barrier overhead from this (again, the book will tell you the gory details).

The barrier overhead varies across compilers and compiler versions, and it depends on the positions of the threads in the machine (e.g., sharing caches or not). You can certainly measure it directly with a suitable microbenchmark [2], but it is quite interesting to see the impact directly in the vector triad performance data.

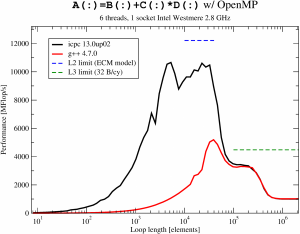
Here we see the OpenMP vector triad performance on one “Intel Xeon Westmere” socket (6 cores) running at about 2.8 GHz, comparing a reasonably current Intel compiler with g++ 4.7.0. With the Intel compiler the sequential code achieves “best possible” performance within the L1 cache (4 flops in 3 cycles). With OpenMP turned on you cannot see this, of course, since the barrier overhead dominates for loop lengths below a couple of 1000s.

Looking at the results for the two compilers we see that GCC has not learned anything over the last five years (this is for how long we have been comparing compilers in terms of OpenMP barrier overhead): The barrier takes roughly a factor of 20 longer with gcc than with the Intel compiler. Comparing with the ECM performance model [3] for the vector triad we see that the Intel compiler’s barrier is fast enough to at least get near the performance limit in the L2 cache (blue dashed line). Both compilers are on par where it’s easy, i.e., in L3 cache and memory, where the loop is so long that the overhead is negligible.

Note that the bad performance of g++ in this benchmark is not due to some “magic” compiler option that I’ve missed. It’s the devastatingly slow OpenMP barrier. For reference, these are the compiler options I have used:

icpc -openmp -Ofast -xHOST -fno-alias ...

g++ -fopenmp -O3 -msse4.2 -fargument-noalias-global ...

In conclusion, the GCC OpenMP barrier is still slooooow. If you have “short” loops to parallelize, GCC is not for you. Of course you might be able to work around such problems (mutilating a popular saying from one of the Great Old Ones: “If synchronization is the problem, don’t synchronize!”), but it’s still good to be aware of them.

If you are interested in concrete numbers you can take a look at any of our recent tutorials [4], where we always include some recent barrier measurements with current compilers.

[1] G. Hager and G. Wellein: Introduction to High Performance Computing for Scientists and Engineers. CRC Press, 2010.

[2] The EPCC OpenMP Microbenchmarks.

[3] G. Hager, J. Treibig, J. Habich, and G. Wellein: Exploring performance and power properties of modern multicore chips via simple machine models. Computation and Concurrency: Practice and Experience, DOI: 10.1002/cpe.3180 (2013), Preprint: arXiv:1208.2908

[4] My Tutorials blog page