Non-temporal stores (also called “streaming stores”) were added to x86 processors with SSE2 (i.e. when the first Pentium IV called “Willamette” appeared in 2000). There was also some support in MMX before, but nobody should be required to use MMX any more. In contrast to standard store instructions which transfer data from registers to memory, NT stores do not require a prior cache line read for ownership (RFO) but write to memory “directly” (well not quite – but to first order it’s true). Beware the usual explanations for RFO that Google finds for you – they almost all describe RFO as something inherently connected to cache coherency in multi-processor systems, but RFO is also required on a single core, whenever there is a cache that is organized in lines.
What are NT stores good for? Again, most references cite them as a means to avoid cache pollution in cases where stored data will not be re-used soon. That’s true to some extent; every word that you don’t store in your cache means more room for other, more frequently used data. But that’s only one half the story. Imagine you have a code whose working set fits into the outer-level cache and which produces data to be stored in memory. Using NT stores for such a code will probably slow it down because, depending on the LD/ST balance, performance is then limited by the memory interface. The true benefit of NT stores can be seen with a truly memory-bound code which is not dominated by loads, like, e.g., the STREAM COPY benchmark, relaxation methods, the lattice-Boltzmann algorithm, or anything that can be formulated in terms of stride-one store streams: By saving the RFO, the pressure on the memory subsystem is reduced. See, e.g., my talk at the KONWIHR results and review workshop in December 2007 at LRZ where the performance boost through NT stores was demonstrated using a 2D Jacobi (5-point stencil) code.
The most important non-temporal store instruction is movntpd, which writes the contents of a full 16-byte SSE register (xmm0…xmm15) to memory. The memory address has to be a multiple of 16, else an exception will be generated. Also, this instruction exists in a “packed” variant only, i.e. there is no movntsd that would only store the lower 8 bytes of the register (AMD has included it, though, into their SSE4a extensions which are implemented with the K10 CPUs – read a nice writeup by Rahul Chaturvedi from AMD for more information). So, if you are stuck with Intel processors or a compiler which does not know about movntsd on K10, loops which use NT stores must be vectorizable and the store stream(s) must be 16-byte aligned.
Or so I thought, for a long time. This assumption was backed, of course, by stupid compilers who blatantly refused to use NT stores if they weren’t 100% sure at compile time whether the store stream was actually aligned. Never heard of loop peeling, eh? Thank goodness great Intel gave us the vector aligned pragma, which you can put in front of a loop in order to tell the compiler that the streams appearing inside the loop were 16-byte aligned! But that always refers to all streams, including reads, and if you somehow forget to pay proper attention, you’re immediately punished by an exception again. To make a long story short, you never really know what’s going on inside the compiler’s twisted little brain, and the diagnostics don’t help either (“LOOP WAS VECTORIZED”, yes, thank you very much).
In hope for some future improvement (unaligned NT store? Or *gasp* maybe even a scalar one?) I looked into Intel’s AVX extensions for SSE, to be implemented in the Sandy Bridge processor, which is to follow Westmere in 2010. That would be a “Streaming SIMD Extension Extension”, right? Whatever, there is neither a scalar nor an unaligned packed NT store in there. But I stumbled across something that had been there since SSE2: The beautiful maskmovdqu instruction. From the manual:
MASKMOVDQU xmm1,xmm2 – Store Selected Bytes of Double Quadword with NT Hint
Stores selected bytes from the source operand (first operand) into an 128-bit memory location. The mask operand (second operand) selects which bytes from the source operand are written to memory. The source and mask operands are XMM registers. The location of the first byte of the memory location is specified by DI/EDI/RDI and DS registers. The memory location does not need to be aligned on a natural boundary. […]
Way cool. Although the fixed address register is somewhat inflexible, the instruction is even better than pure scalar or pure unaligned NT store – it can store any part of an XMM register, down to the byte level, and with no alignment restrictions. And there’s a C/C++ compiler intrinsic, too. That has made it easy to implement our beloved vector triad in explicit SSE. These are two possible variants:
| Scalar (unaligned) |
Packed unaligned |
__m128d xmm1,xmm2,xmm3,xmm4;
__m128i mask_low=_mm_set_epi32(0,0,-1,-1);
#pragma omp parallel private(j)
{
if(size > 1000000) {
for(j=0; j<niter; j++){
#pragma omp for private(xmm1,xmm2,xmm3,xmm4)
for(i=0; i<size; i++) {
xmm1 = _mm_load_sd(d+i);
xmm2 = _mm_load_sd(c+i);
xmm3 = _mm_load_sd(b+i);
xmm4 = _mm_mul_sd(xmm1,xmm2);
xmm4 = _mm_add_sd(xmm4,xmm3);
_mm_maskmoveu_si128(reinterpret_cast<__m128i>(xmm4), mask_low, (char*)(a+i));
}
}
} else {
// same with standard store
}
|
__m128d xmm1,xmm2,xmm3,xmm4;
__m128i mask_all=_mm_set_epi32(-1,-1,-1,-1);
#pragma omp parallel private(j)
{
if(size > 1000000) {
for(j=0; j<niter; j++){
#pragma omp for private(xmm1,xmm2,xmm3,xmm4,xmm5)
for(i=0; i<size; i+=2) {
xmm1 = _mm_load_pd(d+i);
xmm2 = _mm_load_pd(c+i);
xmm3 = _mm_load_pd(b+i);
xmm4 = _mm_mul_pd(xmm1,xmm2);
xmm4 = _mm_add_pd(xmm4,xmm3);
_mm_maskmoveu_si128(reinterpret_cast<__m128i>(xmm4), mask_all, (char*)(a+i));
}
}
} else {
// same with standard store
}
|
The left one is an example for a purely scalar code which employs NT stores. The right one shows how a vectorized code can be endowed with NT stores if 16-byte alignment cannot be enforced. The compiler does neither by itself. Of course, NT stores only make sense if the arrays are large. I have set the lower limit to N=1000000, which is largish compared to the cache sizes but neatly shows the effect of NT vs. standard store:
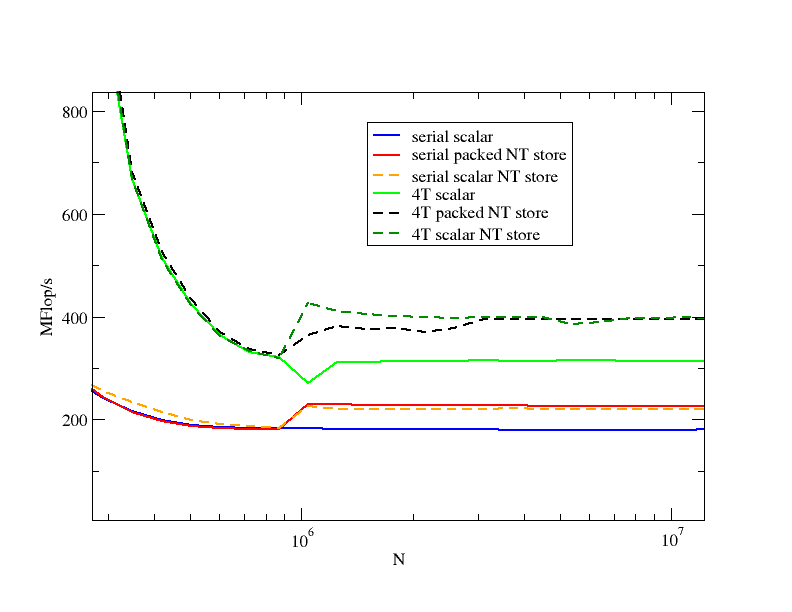
The figure includes standard scalar versions without NT stores as well. Obviously, the maskmovdqu instruction does the job. There is hardly any performance loss in the serial case, and none at all with four threads. I have omitted any comment on in-cache behavior of the different variants; this is a separate story (and one which becomes more interesting once Nehalem is out!).
If you want to know more about using SSE intrinsics in C/C++ code, the Intel C++ Compiler for Linux Intrinsics Reference is for you.