Georg Hager's Blog

Random thoughts on High Performance Computing

Inhalt

Himeno stencil benchmark: Roofline performance modeling and validation

[Update 17/11/29: Pointed out that the C version was modified from the original code – thanks Julian]

The Himeno benchmark [1] is a very popular code in the performance analysis and optimization community. Countless papers have been written that use it for performance assessment, prediction, optimization, comparisons, etc. Surprisingly, there is hardly a solid analysis of its data transfer properties. It’s a stencil code after all, and most of those can be easily analyzed.

The code

The OpenMP-parallel C version looks as shown below. I have made a slight change to the original code: The order of indices on the arrays a, b, and c hinders efficient SIMD vectorization, so I moved the short index to the first position. This also makes it equivalent to the Fortran version.

// all data structures hold single-precision values
for(n=0;n<nn;++n){
  gosa = 0.0;
  #pragma omp parallel for reduction(+:gosa) private(s0,ss,j,k)
  for(i=1 ; i<imax-1 ; ++i)
    for(j=1 ; j<jmax-1 ; ++j)
      for(k=1 ; k<kmax-1 ; ++k){
        // short index on a, b, c was moved up front
        s0 = a[0][i][j][k] * p[i+1][j ][k ]
           + a[1][i][j][k] * p[i ][j+1][k ]
           + a[2][i][j][k] * p[i ][j ][k+1]
           + b[0][i][j][k] * ( p[i+1][j+1][k ] - p[i+1][j-1][k ]
                             - p[i-1][j+1][k ] + p[i-1][j-1][k ] )
           + b[1][i][j][k] * ( p[i ][j+1][k+1] - p[i ][j-1][k+1]
                             - p[i ][j+1][k-1] + p[i ][j-1][k-1] )
           + b[2][i][j][k] * ( p[i+1][j ][k+1] - p[i-1][j ][k+1]
                             - p[i+1][j ][k-1] + p[i-1][j ][k-1] )
           + c[0][i][j][k] * p[i-1][j ][k ]
           + c[1][i][j][k] * p[i ][j-1][k ]
           + c[2][i][j][k] * p[i ][j ][k-1]
           + wrk1[i][j][k];
        ss = ( s0 * a[3][i][j][k] - p[i][j][k] ) * bnd[i][j][k];
        gosa = gosa + ss*ss;
        wrk2[i][j][k] = p[i][j][k] + omega * ss;
      }
  // copy-back loop ignored for analysis
  #pragma omp parallel for private(j,k)
  for(i=1 ; i<imax-1 ; ++i)
    for(j=1 ; j<jmax-1 ; ++j)
      for(k=1 ; k<kmax-1 ; ++k)
        p[i][j][k] = wrk2[i][j][k];
} /* end n loop */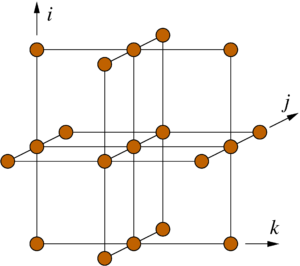

Himeno stancil

Figure 1: Structure of the 19-point stencil showing the data access pattern to the p[][][] array in the Himeno benchmark. The k index is the inner (fast) loop index here.

There is an outer iteration loop over n. The first (parallel) loop nest over i, j, and k updates the wrk2 array from the arrays a, b, c, wrk1, bnd, and p, of which only p has a stencil-like access pattern (see Fig. 1). All others are accessed in a consecutive, cacheline-friendly way. Since the coefficient arrays a, b, and c carry a fourth index in the first position, the row-major data layout of the C language leads to many concurrent data streams. We will see whether or not this impacts the performance of the code.

A second parallel loop nest copies the result in wrk2 back to the stencil array p. This second loop can be easily optimized away (how?), so we ignore it in the following; all analysis and performance numbers pertain to the first loop only.

Amount of work

There are 14 floating-point additions, 7 subtractions, and 13 multiplications in the loop body. Hence, one lattice site update (LUP) amounts to 34 flops.

Data transfers and best-case code balance

For this analysis the working set shall be larger than any cache. It is straightforward to calculate a lower limit for the data transfers if we assume perfect spatial and temporal locality for all data accesses within one update sweep: All arrays except wrk2 must be read at least once, and wrk2 must be written. This leads to (13+1) single-precision floating-point numbers being transferred between the core(s) and main memory. The best-case code balance is thus Bc = 1.65 byte/flop = 56 byte/LUP. If the architecture has a write-back cache, an additional write-allocate transfer must be accounted for if it cannot be avoided (e.g., by nontemporal stores). In this case the best-case code balance is Bc = 1.76 byte/flop = 60 byte/LUP.

Considering that even the most balanced machines available today are not able to feed such a hunger for data (e.g., the new NEC-SX Aurora TSUBASA vector engine with 0.5 byte/flop), we know that this code will be memory bound. If the memory bandwidth can be saturated, the upper performance limit is the memory bandwidth divided by the code balance.

Weiterlesen →

Benchmarking the memory hierarchy of the Intel “Skylake” Xeon E3-1275 v5 using the vector triad

The vector triad results for the AMD Ryzen 1700X in my previous post allowed some interesting conclusions, but it is more instructive to compare them with a current Intel CPU. We have a desktop PC with an Intel “Skylake” Xeon E5-1275 v5 and dual-channel DDR4-2133 memory. This model was introduced in Q4/2015, and it does not support AVX-512 instructions. Although it has only four cores, it is a good fit because it has a similar price tag and power dissipation as the Ryzen 1700X, and it is also built with 14nm technology. The slightly lower theoretical memory bandwidth of 34.1 GB/sec does not really make a difference in practice.

The game is the same as before: I have fixed the clock frequency to 3.0 GHz, and the benchmark is the “throughput-mode vector triad”:

S = get_walltime()
do r=1,NITER
  do i=1,N
    A(i) = B(i) + C(i) * D(i)
  enddo
enddo
WT = get_walltime() - S
MFLOPS = 2.d0 * N * NITER / WT / 1.d6

This was run in parallel, without work sharing, on 1 to 4 cores. Again I have checked that FMA instructions make no difference whatsoever for this extremely data-bound code, and that likwid-bench delivers the same performance levels. An important architectural detail of the Skylake is worth mentioning: Just like its predecessors Haswell and Broadwell, it has a third address generation unit (AGU) for STOREs, hooked to execution port 7. In theory the core can thus sustain two AVX LOADs and one AVX STORE per cycle, doubling the per-cycle data throughput compared to Sandy Bridge and Ivy Bridge. However, Haswell and Broadwell had a limitation on this AGU: It could only process “simple” addresses, i.e., none of the complex addressing modes the Intel compiler uses by default (e.g., [rsi+8*rdx+32]) was able to use the AGU. The compiler (I tried up to version 17.0 update 2) does not know about this and refuses to choose simple addresses at least for the STOREs. By hacking the assembly code I could produce a version using simple addresses for the STOREs; see below for the consequences.

Throughput-mode vector triad on the Skylake chip vs. array length with 1, 2, and 4 cores. Inset: Performance for an in-memory dataset vs. number of cores. The bandwidth numbers assume a code balance of 20 B/flop in all hierarchy levels except L1.

The figure shows the results. I have chosen the same x and y axis ranges as in the Ryzen post, so the comparison should be straightforward:

In the L1 cache the data throughput is at 64 B/cy because the core can sustain either two AVX LOADs or one AVX LOAD and one AVX STORE per cycle. This proves that the third AGU at port 7 cannot be used with compiler-generated code. My “hacked” variant with simple addresses (only using [rcx] for the STOREs, shown as a dotted line) can get to the theoretical limit of 85.3 B/cy (not 96 because the bottleneck is the LOAD port – see any of our recent NLPE tutorials to understand why). But even without port 7 and AVX-512 the Skylake core can outperform the Ryzen by a factor of two per cycle. As a consequence, Skylake can reach the same L1 performance as Ryzen with four (or three, with some port 7 tweaking) instead of eight cores. Well, this was not entirely unexpected.

The large performance breakdown from L1 to L2 is characteristic of Intel architectures because of their “single-ported” L1 cache: In any given cycle, the cache can either talk to the registers or to the L2 cache, but not both. This “feature” was the starting point of our ECM performance model. On Skylake (and Broadwell) the increased L2 bandwidth of 64 B/cy, which was in theory available since Haswell,  can actually be observed [1] (indirectly, of course, due to the non-overlapping L1).  Despite its lower L1 performance, a Ryzen core can easily keep up with the Skylake because of its overlapping cache hierarchy. Due to its eight cores, the Ryzen 1700X has a massively better aggregate L2 performance, of course, and tops out at over 256 B/cy, whereas the Skylake chip stays at just below 160 B/cy.

The L3 cache on the Skylake is, as opposed to Ryzen, bandwidth-scalable up to all 4 cores. The Ryzen’s two “compute complexes” save its neck here because two L3s have two times the bandwidth, so the overall performance level is about 1.6x higher than on Skylake. One could argue that it is unfair to compare a four-core with an eight-core part, but I don’t actually care – this is not a bang-for-the-buck shootout but an architectural comparison.

The memory bandwidth (inset in the figure) shows similar characteristics to the Ryzen: A single core can almost saturate the bandwidth. Actually, if you let Turbo Mode do its thing there is hardly a discernible speedup in memory bandwidth for multiple cores. The Skylake achieves about 84% of the theoretical peak memory bandwidth for this benchmark. Just as on Ryzen, the efficiency goes up dramatically with a read-only benchmark and tops out at an impressive 97%.

Summing up, the Ryzen CPU cannot keep up with current Intel designs in terms of in-core performance with AVX(2) code. On the other hand, its overlapping cache hierarchy and good memory bandwidth (for a desktop chip) can regain a lot of lost ground despite the non-scalable L3 cache. I’m looking forward to the upcoming Naples CPU, although its value for HPC is probably questionable.

 

[1] J. Hofmann, D. Fey, M. Riedmann, J. Eitzinger, G. Hager, and G. Wellein: Performance analysis of the Kahan-enhanced scalar product on current multi- and manycore processors. Concurrency & Computation: Practice & Experience (2016). Available online, DOI: 10.1002/cpe.3921. Preprint: arXiv:1604.01890

 

Benchmarking the memory hierarchy of the new AMD Ryzen CPU using the vector triad

We have recently acquired the brand-new AMD Ryzen 1700X (8 cores, 3.4+ GHz). Reading all the random numbers that people produce with their benchmarks made me sick, so I decided to run something that is well understood: The Schönauer vector triad. Everyone who knows our lectures and tutorials also knows this simple benchmark:

S = get_walltime()
do r=1,NITER
  do i=1,N
    A(i) = B(i) + C(i) * D(i)
  enddo
enddo
WT = get_walltime() - S
MFLOPS = 2.d0 * N * NITER / WT / 1.d6

Performance is reported in Mflops/sec for a wide range of problem sizes N, and NITER is chosen such that the benchmark runs for a sufficiently long time, long enough so that the wall-clock time measurement is accurate. On top of it we usually run the whole thing on different numbers of cores (using an OMP PARALLEL directive, but without worksharing on the inner loop) so we can evaluate the scalability of the different data paths without any adverse effects from OpenMP overhead. All this can be done very easily and efficiently using the likwid-bench microbenchmarking tool, but I have done the triad runs with my own Fortran-based code and checked afterwards that likwid-bench gives the same results.

The Ryzen system is equipped with 2x 16 GB of DDR4-2400 DRAM for a maximum theoretical memory bandwidth of 38.4 GB/sec. For the measurements I fixed the clock speed to 3.0 GHz, although the nominal clock speed is 3.4 GHz. The reason is simply my current inability to keep the CPU from running in Turbo mode when I set it to 3.4 GHz; it doesn’t matter for the benchmarks, though, because all in-cache numbers will be converted to bytes per cycle, and the memory bandwidth does not (significantly) depend on the clock frequency. I used the Intel compiler version 17.0 Update 2, which generates very decent AVX code on the chip if you give it the -Ofast -xHost options. Using FMAs would not make a difference because the Ryzen core executes a full-width 256-bit FMA in two chunks of 128 bits (and I have checked using likwid-bench that the FMA code runs exactly as fast as the non-FMA version). Besides, this code is totally bound by the data transfers even with data in the L1 cache. I have not used non-temporal store instructions; this is a topic for a future post.

Throughput-mode vector triad on the Ryzen chip vs. array length with 1, 2, 4, and 8 cores. Inset: Performance vs. number of cores for an in-memory dataset. The bandwidth numbers assume a code balance of 20 B/flop in all hierarchy levels except L1.

Now for the data. The figure shows the usual stuff: Performance vs. array size for different numbers of threads (i.e., physical cores – SMT was ignored for this test). Here is my interpretation of the data:

With data in the L1 cache we get very close to 6 Gflops/sec per core, which amounts to a limit of 32 B/cy. Actually, the slide I stumbled across in the AMD booth at SC16 says “2 x 16B LOAD”, while another one says “2 LOADs & 1 STORE per cycle”. I don’t know how they want to sustain this with only two address generation units (AGUs), and the measured data is in line with a limit of “two 16-B LOADs OR one 16-B LOAD and one 16-B STORE per cycle,” identical to SSE limits on Intel Sandy Bridge and Ivy Bridge. If anyone can tell me how to get to the 8 Gflops/sec that can be expected if the 2LD+1ST story were true, go ahead. (Update: The two AGUs would be OK for one AVX LOAD and one half AVX STORE per cycle, just as on Sandy and Ivy Bridge; this would also lead to a maximum triad performance of 8 flops in 3 cycles. However, I can’t see it although the code is definitely AVX).

Between N=1024 and N=16384 the data comes from the 512 KiB per-core L2 cache. The drop in performance occurs at the same N independently of the core count, because we run the benchmark in “throughput mode”, i.e., with the same data size N on each core (think “weak scaling”). You can’t see it in the single-core data on this graph, but the 8-core runs tells us that the L2 actually delivers a little more than 32 B/cy. I have assumed here that there is a write-allocate for every store miss in the L1, increasing the code balance from 16 B/flop to 20 B/flop. The AMD slides linked above are a little cloudy on the details, they only state “32 B/cy” above two arrows between L1 and L2, so it isn’t clear whether this is 32 B/cy per direction or not. Another explanation could be that the write-allocate is optimized away by the hardware if it detects in its line fill buffers a write miss on a cache line that will be completely overwritten. We don’t know for sure, but once likwid-perfctr is ported to the architecture it should be able to shed some light on this.

Another important observation about the L2 (and also the L3): Data transfers overlap quite efficiently with retired LOADs in the L1. If you know the ECM performance model [1] you know that this is not at all the case on current Intel CPUs, making the AMD caches very effective (the IBM Power8 also behaves like this [2]).

The L3 cache is not core-local, but 8 MiB of shared L3 are available to each of the two four-core “core complexes” (CCX). The data clearly reflects this organization: Since I have pinned the threads in core order, i.e., filling one CCX first and then the other, this means we observe a performance drop beyond N=218 on a single core and beyond N=216 on the four cores of one CCX. Nothing changes from four to eight, however, because we get another 8 MiB of L3.

The most important observation about the L3 cache is that its bandwidth does not scale from one to four cores. There is only a slight speedup from 2 to 4, and it tops out at slightly above 64 B/cy assuming a code balance of 20 B/flop. The L3 is also a victim cache, i.e., only cache lines overflowing from the higher-level caches end up there. We will see how the efficiency of the L3 can be influenced by optimizations (such as, e.g., prefetch instructions, which I haven’t used at all here). The L3 bandwidth scales, of course, from 4 to 8 cores simply because there are two L3s.

Finally, the memory bandwidth behavior. This chip has the (IMO very attractive) property that a single core can almost saturate the memory bandwidth of the full chip. Intel desktop CPUs (but not the Xeons) behave in a similar way. The inset in the figure shows performance vs. number of cores for large N. The best bandwidth on a single CCX is obtained with two cores, and there is a slight drop for 3 and 4. We may speculate that this is a faint echo of the non-scalable L3 cache, but there may be many other reasons. With all eight cores we top out at just below 30 GB/sec, which is 77% of the theoretical memory bandwidth (dashed line in the inset). A read-only benchmark yields almost 90%, so it seems that the Ryzen also shares this feature with current Intel chips: the more read-dominated the code, the closer we can get to the peak memory bandwidth. The best overall chip bandwidth is obtained with two threads, one running on each CCX.

My next post will show the same test on a Skylake-type chip for comparison.

[1] H. Stengel, J. Treibig, G. Hager, and G. Wellein: Quantifying performance bottlenecks of stencil computations using the Execution-Cache-Memory model. Proc. ICS15, the 29th International Conference on Supercomputing, June 8-11, 2015, Newport Beach, CA. DOI: 10.1145/2751205.2751240. Preprint: arXiv:1410.5010

[2] J. Hofmann, D. Fey, M. Riedmann, J. Eitzinger, G. Hager, and G. Wellein: Performance analysis of the Kahan-enhanced scalar product on current multi- and manycore processors. Concurrency & Computation: Practice & Experience (2016). Available online, DOI: 10.1002/cpe.3921. Preprint: arXiv:1604.01890

Stepanov test faster than light?

If you program in C++ and care about performance, you have probably heard about the Stepanov abstraction benchmark [1]. It is a simple sum reduction that adds 2000 double-precision floating-point numbers using 13 code variants. The variants are successively harder to see through by the compiler because they add layers upon layers of abstractions. The first variant (i.e., the baseline) is plain C code and looks like this:

// original source of baseline sum reduction
void test0(double* first, double* last) {
  start_timer();
  for(int i = 0; i < iterations; ++i) {
    double result = 0;
    for (int n = 0; n < last - first; ++n) result += first[n];
    check(result);
  }
  result_times[current_test++] = timer();
}

It is quite easy to figure out how fast this code can possibly run on a modern CPU core. There is one LOAD and one ADD in the inner loop, and there is a loop-carried dependency due to the single accumulation variable result. If the compiler adheres to the language standard it cannot reorder the operations, i.e., modulo variable expansion to overlap the stalls in the ADD pipeline is ruled out. Thus, on a decent processor such as, e.g., a moderately modern Intel design, each iteration will take as many cycles as there are stages in the ADD pipeline. All current Intel CPUs have an ADD pipeline of depth three, so the expected performance will be one third of the clock speed in GFlop/s.

If we allow some deviation from the language standard, especially unsafe math optimizations, then the performance may be much higher, though. Modulo variable expansion (unrolling the loop by at least three and using three different result variables) can overlap several dependency chains and fill the bubbles in the ADD pipelines if no other bottlenecks show up. Since modern Intel CPUs can do at least one LOAD per cycle, this will boost the performance to one ADD per cycle. On top of that, the compiler can do another modulo variable expansion for SIMD vectorization. E.g., with AVX four partial results can be computed in parallel in a 32-byte register. This gives us another factor of four.

Original baseline assembly code
-O3 -march=native -O3 -ffast-math -march=native 
  vxorpd %xmm0, %xmm0, %xmm0
.L17:
  vaddsd (%rax), %xmm0, %xmm0
  addq $8, %rax
  cmpq %rbx, %rax
  jne .L17
 
  vxorpd %xmm1, %xmm1, %xmm1
.L26:
  addq $1, %rcx
  vaddpd (%rsi), %ymm1, %ymm1
  addq $32, %rsi
  cmpq %rcx, %r13
  ja .L26
  vhaddpd %ymm1, %ymm1, %ymm1
  vperm2f128 $1, %ymm1, %ymm1, %ymm3
  vaddpd %ymm3, %ymm1, %ymm1
  vaddsd %xmm1, %xmm0, %xmm0

Now let us put these models to the test. We use an Intel Xeon E5-2660v2 “Ivy Bridge” running at a fixed clock speed of 2.2 GHz (later models can run faster than four flops per cycle due to their two FMA units). On this CPU the Stepanov peak performance is 8.8 GFlop/s for the optimal code, 2.93 GFlop/s with vectorization but no further unrolling, 2.2 GFlop/s with (at least three-way) modulo unrolling but no SIMD, and 733 MFlop/s for standard-compliant code. The GCC 6.1.0 was used for all tests, and only the baseline (i.e., C) version was run.
Manual assembly code inspection shows that the GCC compiler does not vectorize or unroll the loop unless -ffast-math allows reordering of arithmetic expressions. Even in this case only SIMD vectorization is done but no further modulo unrolling, which means that the 3-stage ADD pipeline is the principal bottleneck in both cases. The (somewhat cleaned) assembly code of the inner loop for both versions is shown in the first table. No surprises here; the vectorized version needs a horizontal reduction across the ymm1 register after the main loop, of course (last four instructions).

Original baseline code performance
g++ options Measured [MFlop/s] Expected [MFlop/s]
-O3 -march=native 737.46 733.33
-O3 -ffast-math -march=native 2975.2 2933.3

In defiance of my usual rant I give the performance measurements with five significant digits; you will see why in a moment. I also selected the fastest among several measurements, because we want to compare the highest measured performance with the theoretically achievable performance. Statistical variations do not matter here. The performance values are quite close to the theoretical values, but there is a very slight deviation of 1.3% and 0.5%, respectively. In performance modeling at large, such a good coincidence of measurement and model would be considered a success. However, the circumstances are different here. The theoretical performance numbers are absolute upper limits (think “Roofline”)! The ADD pipeline depth is not 2.96 cycles but 3 cycles after all. So why is the baseline version of the Stepanov test faster than light? Can the Intel CPU by some secret magic defy the laws of physics? Is the compiler smarter than we think?

A first guess in such cases is usually “measuring error,” but this was ruled out: The clock speed was measured by likwid-perfctr to be within 2.2 GHz with very high precision, and longer measurement times (by increasing the number of outer iterations) do not change anything. Since the assembly code looks reasonable, the only conclusion left is that the dependency chain on the target register, which is completely intact in the inner loop, gets interrupted between iterations of the outer loop because the register is assigned a new value. The next run of the inner loop can thus start already before the previous run has ended, leading to overlap. A simple test supports this assumption: If we cut the array size in half, the relative deviation doubles. If we reduce it to 500, the deviation doubles again. This strongly indicates an overlap effect (absolute runtime reduction) that is independent of the actual loop size.

In order to get a benchmark that stays within the light speed limit, we modify the code so that the result is only initialized once, before the outer loop:

// modified code with intact (?) dependency chain
void test0(double* first, double* last) {
  start_timer();
  double result = 0; // moved outside
  for(int i = 0; i < iterations; ++i) {
    for (int n = 0; n < last - first; ++n) result += first[n];
    if(result<0.) check(result);
  }
  result_times[current_test++] = timer();
}

The result check is masked out since it would fail now, and the branch due to the if condition can be predicted with 100% accuracy. As expected, the performance of the non-SIMD code now falls below the theoretical maximum. However, the SIMD code is still faster than light.

Modified baseline code performance
g++ options Measured [MFlop/s] Expected [MFlop/s]
-O3 -march=native 733.14 733.33
-O3 -ffast-math -march=native 2985.1 2933.3

How is this possible? Well, the dependency chain is doomed already once SIMD vectorization is done, and the assembly code of the modified version is very similar to the original one. The horizontal sum over the ymm1 register puts the final result into the lowest slot of ymm0, so that ymm1 can be initialized with zero for another run of the inner loop. From a dependencies point of view there is no difference between the two versions. Accumulation into another register is ruled out for the standard-conforming code because it would alter the order of operations. Once this requirement has been dropped, the compiler is free to choose any order. This is why the -ffast-math option makes such a difference: Only the standard-conforming code  is required to maintain an unbroken dependency chain.

Of course, if the g++ compiler had the guts to add another layer of modulo unrolling on top of SIMD (this is what the Intel V16 compiler does here), the theoretical performance limit would be ADD peak (four additions per cycle, or 8.8 GFlop/s). Such a code must of course stay within the limit, and indeed the best Intel-compiled code ends up at 93% of peak.

Note that this is all not meant to be a criticism of the abstraction benchmark; I refuse to embark on a discussion of religious dimensions. It just happened to be the version of the sum reduction I have investigated closely enough to note a performance level that is 1.3% faster than “the speed of light.”

[1] http://www.open-std.org/jtc1/sc22/wg21/docs/D_3.cpp

 

Intel vs. GCC for the OpenMP vector triad: Barrier shootout!

We use the Schönauer Vector Triad for most of our microbenchmarking. It’s a simple benchmark that everyone can write. It looks quite simple when parallelized with OpenMP:

double precision, dimension(N) :: a,b,c,d
! initialization etc. omitted
s = walltime()
!$omp parallel private(R,i)
do R=1,NITER
!$omp do
  do i=1,N
    a(i) = b(i) + c(i) * d(i)
  enddo
!$omp end do
enddo
!$omp end parallel
e=walltime()
MFlops = R*N/(e-s)/1.e6

There are some details that are necessary to make it work as intended; you can read all about this in our book [1]. Usually we choose NITER for every N so that the runtime is a couple hundred milliseconds (so it can be measured accurately), and report performance for N ranging from small to large. The performance of the vector triad is determined by the data transfers, even when the data is in the L1 cache. In the parallel case we can additionally see the usual multicore bandwidth bottleneck(s).

The OpenMP parallelization adds its own overhead, of course. As it turns out, it is mostly concentrated in the implicit barrier at the end of the workshared loop in this case. So, when looking at the performance of the OpenMP code vs. N, we usually see that using more threads slows down the code if N is too small. We can even calculate the barrier overhead from this (again, the book will tell you the gory details).

The barrier overhead varies across compilers and compiler versions, and it depends on the positions of the threads in the machine (e.g., sharing caches or not). You can certainly measure it directly with a suitable microbenchmark [2], but it is quite interesting to see the impact directly in the vector triad performance data.

vtriad_Lima_icpc_vs_gcc

Here we see the OpenMP vector triad performance on one “Intel Xeon Westmere” socket (6 cores) running at about 2.8 GHz, comparing a reasonably current Intel compiler with g++ 4.7.0. With the Intel compiler the sequential code achieves “best possible” performance within the L1 cache (4 flops in 3 cycles). With OpenMP turned on you cannot see this, of course, since the barrier overhead dominates for loop lengths below a couple of 1000s.

Looking at the results for the two compilers we see that GCC has not learned anything over the last five years (this is for how long we have been comparing compilers in terms of OpenMP barrier overhead): The barrier takes roughly a factor of 20 longer with gcc than with the Intel compiler. Comparing with the ECM performance model [3] for the vector triad we see that the Intel compiler’s barrier is fast enough to at least get near the performance limit in the L2 cache (blue dashed line). Both compilers are on par where it’s easy, i.e., in L3 cache and memory, where the loop is so long that the overhead is negligible.

Note that the bad performance of g++ in this benchmark is not due to some “magic” compiler option that I’ve missed. It’s the devastatingly slow OpenMP barrier. For reference, these are the compiler options I have used:

icpc -openmp -Ofast -xHOST -fno-alias ...
g++ -fopenmp -O3 -msse4.2 -fargument-noalias-global ...

In conclusion, the GCC OpenMP barrier is still slooooow. If you have “short” loops to parallelize, GCC is not for you. Of course you might be able to work around such problems (mutilating a popular saying from one of the Great Old Ones: “If synchronization is the problem, don’t synchronize!”), but it’s still good to be aware of them.

If you are interested in concrete numbers you can take a look at any of our recent tutorials [4], where we always include some recent barrier measurements with current compilers.

[1] G. Hager and G. Wellein: Introduction to High Performance Computing for Scientists and Engineers. CRC Press, 2010.

[2] The EPCC OpenMP Microbenchmarks.

[3] G. Hager, J. Treibig, J. Habich, and G. Wellein: Exploring performance and power properties of modern multicore chips via simple machine models. Computation and Concurrency: Practice and Experience, DOI: 10.1002/cpe.3180 (2013), Preprint: arXiv:1208.2908

[4] My Tutorials blog page

Fooling the masses – Stunt 12: Redefine “performance” to suit your needs!

(See the prelude for some general information on what this is all about)

There is actually a very clear definition of the term “performance” in HPC: “performance” is “work” divided by “time.” You may think about “work” as “the problem”; occasionally, Flops is a possible (but easily manipulable) measure. “Time” is the overall wall-clock time to do the work, including everything that needs to be done but counts as overhead, such as communication and synchronization. If you look at performance with respect to parallel resources, i.e., if you want to know how performance scales with the number of workers, the same formula applies – to strong and to weak scaling alike.

Now sometimes the performance results for your parallel program are … mediocre. There may be two reasons for this:

  • Scalability is good but your single-core or single-node performance sucks. This is may be a consequence of your applying stunt 2, either by accident or on purpose. If you only show speedups (see stunt 1) you will be fine; however, sometimes it is not so easy to get away with this.
  • Single-core and single-socket performance is good (i.e., you understand and hit the relevant bottleneck[s]), but scalability is bad. You know the culprits: load imbalance, insufficient parallel work, communication, synchronization.

Either way, you probably don’t want to show actual performance numbers or data about time to solution. As it happens there is a host of options you can choose from. You can certainly play around with the “time” component in the performance calculation, as shown in stunt 5 and stunt 9, or quietly invoke weak scaling as shown in stunt 4. Here are some popular and more imaginative examples:

Employ “floptimization:” Throw in some extra Flops to make the CPU perform more “work” at hardly any extra cost; often there is at least some headroom in the floating-point pipelines when running real applications. Accumulating something in a register is a classic:

  for(s=0.0, i=0; i<N; ++i) {
    p[i] = f(q[i]); // actual work
    s += p[i];      // floptimization
  }

Even if the sum over all elements of p[] is not needed at all, it’s one more Flop per iteration, it boosts your flop rate, and it will usually not impact your time to solution! If you do it right, only the sky is the limit.

Use manpower metrics: Developing code is expensive, so you can take manpower into account. State that your superior hardware or software environment enabled you to get a working code in less than one week, which amounts to so and so many “man-hours per GFlop/s.” This can be extended to other popular software metrics.

Play the money card: “GFlop/s per Dollar” may also be useful, especially if you compare different systems such as your average off-the-shelf departmental cluster and the big DoE-paid iron.

Go green: Since everyone in HPC today is all mad about saving energy, use “Joules per Flop,” “GFlop/s per Watt,” “CO2 equivalents,” “Joule-seconds,” “Joule-seconds-squared,” or any other combination of metrics that shows the superiority of your approach in terms of “green” or “infrastructure-aware” computing. Moreover, energy to solution is almost proportional to runtime, so you can rename your paper on “Performance Optimization of a Kolonovski-Butterfield Solver” to “Energy Optimization of a Kolonovski-Butterfield Solver” and turn a boring case study into bleeding-edge research.

Blame the wimpy hardware: For multi- or many-core chips, per-core or per-thread metrics mask the inherent bottlenecks and are great for bashing your competitors. For instance, when comparing a multi-core CPU with a GPGPU you could declare that “the available bandwidth per thread is 122 times higher on the CPU than on the GPGPU.” Oh wait – make that 121.68 times.

taskmgr.png

Figure 1: Windows task manager is your friend: Four cores, all of them 100% utilized – that’s performance!

Boast frantic activity: MIPS (millions of instructions per second) or, equivalently, IPC (instructions per cycle) are perfect higher-is-better metrics if true performance is low. IPC can be boosted on purpose by several means: You can use a highly abstracting language to make the compiler generate a vast amount of instructions for simple things like loading a value from memory, or disable SIMD so that more instructions are executed for the same amount of work. Waiting in OpenMP barriers or MPI functions is also good for a large IPC count, since it often involves spin-waiting loops. You can use special options to disable compiler optimizations which have the potential to change numerical results (such as common subexpression elimination). But take care: If that means moving slow operations like floating-point divides into an inner loop, the IPC value will go down dramatically.

Fight the evil: State that your new code or new algorithm shows a factor of X fewer cache misses compared to the baseline. Cache misses are the black plague of HPC, so nobody will doubt your success. And they are just as easy to manipulate as Flops. Combining with the “go green” strategy is straightforward: Cache misses cost vast amounts of energy (they say), so you can be green and good at the same time!

Wow the management: State that “all processors are 100% utilized, so the code makes perfect use of the available resources.” Windows task manager is the perfect tool to show off with a stunt like this (see Fig. 1), but “top” under Linux works fine, too:

  PID VIRT RES  SHR %CPU %MEM  TIME+  P COMMAND 
 2318 492m 457m 596 98.6 22.9 0:35.52 2 a.out 
 2319 492m 457m 596 98.6 22.9 0:35.53 0 a.out 
 2321 492m 457m 596 98.6 22.9 0:35.50 1 a.out 
 2320 492m 457m 596 97.6 22.9 0:35.44 3 a.out

In summary, metrics are your wishing well: Find the right metric and any code will look good.

This stunt is essentially #9 of Bailey’s original “Twelve ways to fool the masses.”

Fooling the masses – Stunt 11: Show data! Plenty. And then some.

(See the prelude for some general information on what this is all about)

ShowDataPlenty_Bars

Figure 1: Lots of variants of an experiment, lots of machines, no idea for interpretation – why not show it all?

Computers produce data. Parallel computers produce more data. And doing performance experiments with parallel computers produces even more data, since we often conduct several runs with different code variants on different machines. Now imagine a situation where you’ve got all this data lying around on your disk, but you can’t make any sense of it. Since you wouldn’t bother to establish even a coarse performance model (your setup is just too complex for this kind of bean counting), you don’t know whether some particular performance measurement is “good” or “bad” on some particular machine, or how performance should change when some parameter is altered.

Why not put the cart before the horse and show all the data? This has decisive advantages: You can display all the work you did, without the embarrassing message that five or six numbers is all the relevant data you got from your research. Furthermore, it gives you the opportunity to add “discussion” at any desirable level of detail. For instance, if the page limit for submitting to your favorite conference is ten pages, and you have five pages full of messy bar graphs (such as the one shown in Fig. 1), you can easily fill the rest with meaningless “explanations” like “Variant 11 shows about 90% performance advantage on Machine G over Variant 10 on Machine F while, surprisingly, Variant 9 on Machine A is 6% slower than Variant 7 on Machine C.” You may want to write “92.23%” and “5.982%” here – see Stunt 8 for the reason.

In Summary, you can make up for your lack of insight by showing data. Plenty of it. Swamp your readers or your audience with hundreds of colorful bar graphs, scatter plots, timing diagrams, or whatever your favorite data visualization tool has to offer, and describe them at length. If you really want to leave the impression of true understanding, resort to obscure technical details − but this is the theme of another stunt.

 

Fooling the masses – Stunt 8: Impress your audience with awe-inspiring accuracy

(See the prelude for some general information on what this is all about)

“Qualitative” statements make you cringe. Being a scientist, you know that science is all about accuracy. And what could be more accurate than numbers?  Good for you! There is ample opportunity for generating numbers in computer science. The art is to not block your audience’s view on the raw and unfiltered truth.

# cores Time (plain) [s] Time (optimized) [s] Speedup [%]
1 12.0435766 8.6198441 39.71919283
2 6.1179025 5.5901951 9.439874469
3 4.9041394 4.6966098 4.418710705
4 4.7002801 4.6912042 0.193466317

Fig. 1: Awesome! Up to 1.77992 times faster!

A simple example: When comparing performance numbers between different machines or code versions (see Stunt 7 for some amazing tricks you can play there), don’t hesitate to provide timings with sub-microsecond resolution, even if the results fluctuate like mad. Then state, in a slightly generalizing, “management-style” demeanor, that your “optimizations lead to a performance increase of up to 39.71919283%”, and refer to the data (see the table) to substantiate your assertion. In other words, forget what your high school teachers told you about significant digits and use the full power of your pocket calculator, even if a slide rule would also do the trick.

By the way, the same works for drawing conclusions from data in diagrams. Since it is sometimes hard to read off precise values from graphs, help your audience by stating the raw facts (see Fig. 1). Using boldface and jazzy colors will help to keep peoples’ attention on the important messages. Do not waste time and space dealing with lengthy explanations but let the numbers speak for themselves!

 

Sun UltraSPARC T2 under test

Thanks to Sun Microsystems and the kind people from RWTH Aachen we had access to a pre-production UltraSPARC T2 (a.k.a. “Niagara 2”) system for some tests. We didn’t manage to get the whole RRZE benchmark suite running but could produce some pretty interesting low-level stuff. The peculiar way the N2 addresses its four built-in memory controllers leads to severe congestion if the mutual alignment of memory streams is unfortunate. This can be seen, e.g. with Lattice-Boltzmann codes and, of course, also with STREAM.

That said, if you know what you’re doing and somehow manage to get what we have learned into applications, the Niagara2 is a pretty interesting processor. In a single socket it has a nominal memory bandwidth of >60 GB/s (40 read, 20 write) of which about a third can be actually measured. At a peak performance of 11 GFlop/s (8 cores at 1.4 GHz), this makes for a pretty impressive machine balance which is far beyond any other cache-based CPU. And finally, the multi-threaded architecture is much less strange and hard to grasp than, e.g., the Cell design.

If you want to know more, here’s a presentation we prepared for the recent “SunDay” at RRZE. Please bear in mind that all of this is still preliminary data and will have to be confirmed on production hardware.

rrze-n2-ea.pdf

All about the N2’s microarchitecture can be found in this neat document:
http://opensparc-t2.sunsource.net/specs/OpenSPARCT2_Core_Micro_Arch.pdf